機動學HW13

13.1 試設計一組複式齒輪，使其轉速比為125（請說明思考步驟及結果）

若要設計一個轉速比為125的齒輪系統，有可能放大系統就是所謂的高速齒輪比，motor的齒輪轉一圈，而傳動齒輪就轉125圈。若是縮小系統就是所謂的扭力齒輪比，motor齒輪轉125圈，而傳動齒輪才轉一圈。上面差別只在於motor式以哪一齒輪為主動，就能造成極大的差異。齒輪比為125，那直觀上就是5的3次方，就代表說齒輪只要連接三個1:5的齒輪組就可已達到1:125效果。



齒輪一 　齒輪二　　齒輪三　　齒輪四

ratio　 1 5 25 125 　



但上面直觀的想法雖能很容易達到齒輪比為125，但是所用齒輪數過多會造成動力的耗損。因此若能減少齒輪數，就可以減少動力耗損。若以三個齒輪為系統，125開根號為11.1803，因此只要兩組11.1803的齒輪就可以達到效果，並減少動力耗損。



齒輪一 　齒輪二　　齒輪三　　
ratio　 1 11.1803 125





第五次作業和第九次作業是我最得意的，第五次作業結合了老師上課所用講議之外，而把老師程式看懂之後，在運用老師的程式在結合自己所寫的程式，就可以做出新的動畫，這樣激發自己動腦寫程式，而把它寫出來是有一種成就感。而第九次作業用老師程式在加上自己分析之後所作之程式跑出動畫，而且做了詳盡的分析，是我作業作的最詳盡的ㄧ次。





　

機動學HW12

一組標準全齒輪齒輪之徑節為8（亦可使用自設值），齒數分別為30T與48T，其工作壓力角為20度（可為14.5或25度，自選）。
以之齒倫之條件，因此只要帶入齒輪比公式及可求出答案，而此題可用 講義中的contact_ratio算出答案，而帶入數值
Pd(徑節)=8
n2,n3(兩齒輪之齒數)30、48
phi(壓力角)20
[c_ratio, c_length,ad,pc,pb,r2,r3,ag]=contact_ratio(Pd,n2,n3,phi)

接觸比c_ratio = 1.7005

接觸長度c_length = 0.6275

齒冠ad = 0.1250

周節pc = 0.3927

基周節pb = 0.3690

兩齒輪節圓直徑。r2 = 3.7500 r3 = 6

兩齒輪之接近角、遠退角及作用角
ag = 10.4850 9.9211 20.4061
6.5532 6.2007 12.7538


節圓(pitch circle):節面之正頗面，代表齒輪之虛擬圓。
已知壓力角20度、勁節為8 齒數30T、40T
r1(節圓半徑)= 30/(2*8)=1.875　
r2(節圓半徑)= 48/(2*8)=3　

基圓(base circle)：虛擬圓，用以產生漸開線已形成齒形。
rb1=r1(節圓半徑)*cos20=1.7619
rb2=r2(節圓半徑)*cos20=2.5980


干涉之證明
測試干涉之條件為：
(N2+2N2 x N3)(sinΦ)^2＞= 4 + 4N3
設N2=30T N3=48T，Φ=20度
30(30+2*48)*(sin(20))^2)＞4(1+48)
並不會有干涉。
也可用講議之程式

function [x]=isinterf(phi,N1,N2)
%
% Test if the gear set exists an interference
% phi:pressure angle, in degrees
% N1,N2:teeth of both gears
% x=0:no interference; x=1 interence exists
x=0;
sinx=sin(phi*pi/180);
if N2＜N1,nn=N1;N1=N2;N2=nn;end
if N1*(N1+2*N2)*sinx*sinx＜4*(1+N2), x=1;end

isinterf(20,30,48)
ans = 0 (不為干涉)

用draw_gear.m畫出接合情形，而只要把齒輪角度做些修改即可。
壓力角為20度




用講義中之程式
function move2_gear(Dpitch,nn1,nn2,phi,omega1)
% move2_gear(Dpitch,nn1,nn2,phi,omega1)
% To draw a whole gear.
% Inputs:
% Dpitch:dimetral pitch
% nn1,nn2: no. of teeth for both gears
% phi:pressure angle, degrees
% omega1: angular velocity of gear 1
move2_gear(8,30,48,20,10)
做出動畫

機動學HW11

Part1
圖輪為滯留時且rmp=0時，則位移、速度、加速度都為０因此在使用function　parabol_cam就可以畫出圖輪角度與位移、速度、加速度、之關係。

function [y, yy, yyy]=parabol_cam(phi, phi_in, beta_range, direct, travel,rpm)
%y為位移　yy為速度　yyy為加速度
%phi 輸入角度
%phi_in起始角度
%beta_range角度的範圍
%direct=1為上升　direct=-1為下降
%travel上升的位移
%rmp角速度
d2r=pi/180;
th=phi*d2r; thinit=phi_in*d2r; beta=beta_range*d2r;
speed=rpm*2*pi/60;if rpm==0, speed=1;end;
theta=th-thinit;
thmed=thinit+beta/2;
thx=theta/beta;
if direct==1,
if th＜thmed
y=2*thx^2;
yyy=4/beta/beta;
yy=yyy*th;
else
y=1-2*(1-thx)^2;
yy=4/beta*(1-thx);
yyy=-4/beta/beta;
end
else
if th＜thmed
y=1-2*thx^2;
yyy=-4/beta/beta;
yy=yyy*th;
else
y=2*(1-thx)^2;
yy=-4/beta*(1-thx);
yyy=4/beta/beta;
end
end
y=y*travel;
yy=yy*speed*travel;
yyy=yyy*speed*speed*travel;

某凸輪開始時先在0-100∘區間滯留，然後提升後在200至260∘區間滯留，其高度（衝程）為5公分，其餘l由260∘至360∘則為返程。
運用講義裡的parabol_cam程式畫成關係圖，下面為自己所做程式
function cam
for i=1:10
ss(i)=0;
vv(i)=0;
aa(i)=0;
end;
for i=11:21
phi=(i-1)*10;
[ss(i),vv(i),aa(i)]=parabol_cam(phi,100,100,1,5,0);
end;
for i=22:26
ss(i)=30;
vv(i)=0;
aa(i)=0;
end;
for i=27:1:37
phi=(i-1)*10;
[ss(i),vv(i),aa(i)]=parabol_cam(phi,260,100,-1,5,0);
end;
w=0:10:360;
figure
plot(w,ss,'o-','LineWidth',2);
figure
plot(w,vv,'ko-','LineWidth',2);
figure
plot(w,aa,'ro-','LineWidth',2);

位移與角度關係圖

速度與角度關係圖


加速度與角度關係圖


Part2
設凸輪之半徑為15公分，以順時針方向旋轉，其從動件為梢型，垂直接觸，長為10公分，從動件之運動係依照第二項之運動型式。試繪出此凸輪之工作曲線。
需注意的是，此曲線的起始點不為0，而是25(圖輪半徑加上鞘的長度)

位移與角度關係圖


part3

依照上面凸輪的條件而繪出下面動畫

function run
for i=1:100
    r(i)=15;
end
for i=101:201
    r(i)=15+(5/100)*(i-100);％畫出半徑長
end
for i=201:260
    r(i)=20;
end
for i=261:360
    r(i)=20-(5/100)*(i-260);%畫出半徑長
end
theta=linspace(0,2*pi,360);
for i=1:360
   k=r(1);
for j=1:359
    r(j)=r(j+1);%元素取代
end
r(360)=k;
polar(theta,r);%用及坐標繪出圖形
pause(0.00001)
end

下面為圖輪動畫

機動學hw10

Part1

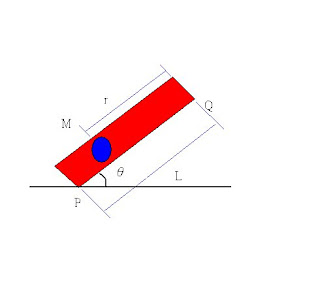若以M為固定點，做逆時針旋轉，假設為等假角速度ω，則Vp=(ω) x (r)，若以複數座標表示iωr*exp(iωt+iθ)，而向心加速度為-(ω^2) x (r)以複數座標表示為-ω*ω*r*exp(iωt+iθ)。若從Q點看P點的速度為Vp=Vq +(ω) x (r)。若在M點有一水平速度，則P點速度為Vp=Vo + (ω) x (r) 若以複數座標表示v+iωr*exp(iωt+iθ)。若在M點同時有水平加速度，則P點速度為Vp=Vo+at+v+(ω) x (r)若以複數座標表示為v+at+iωＸ*exp(iωt+iθ)，加速度為a=a-(ω^2) x (r)，以複數座標形式為a-ω*ω*Ｘexp(iωt+iθ)。如果速度和加速度不為水平的，則只要分成水平方向和垂直方向。

四連桿的狀況
P以A為旋轉中心
Q以B為旋轉中心所以　
PQ　的速度方向　
如圖示都分別為桿子垂直方向

Part2

由於偏至量e為０，而若曲桿要旋轉一圈，則R>L，因此下面動畫是以R=15 L=20，而當曲桿與水平面垂直時，以機動課本圖，舜心１３點會交於無限遠。如動畫所呈現紅色圓圈為瞬心的位置

下面為畫出動畫的程式

%Example:slider_draw2(15,20,0)
function slider_draw2(R,L,e)
ang=linspace(0,360,100);
[d,theta3]=slider_solve(ang,R,L,e,1)
x=R*cosd(ang);
y=R*sind(ang);
for n=1:100
link_plot([0,x(n),d(n)],[0,y(n),e],2);
line([d(n)-3,d(n)+3,d(n)+3,d(n)-3,d(n)-3],[e-2,e-2,e+2,e+2,e-2]);
hold on
plot(0,0,'ro')
plot(x(n),y(n),'ro')
plot(d(n),e,'ro')
plot([0,0],[0,e-d(n)*(y(n)-e)/(x(n)-d(n))],'ro:') %算出瞬心點到連桿之間連線
plot([x(n),0],[y(n),e-d(n)*(y(n)-e)/(x(n)-d(n))],'ro:') %算出瞬心點連桿之間連線
plot([x(n),d(n)],[y(n),y(n)*d(n)/x(n)],'ro:')
plot([d(n),d(n)],[0,y(n)*d(n)/x(n)],'ro:')
axis equal
axis ([-45 45 -30 30]);
pause(0.05)
clf
end

以slider_draw2(15,20,0)跑出動畫為

機動學HW9

偏置滑塊機構是滑塊之滑動方向與水平方向有ㄧ距離e，此稱偏置量，而偏置量會影響滑塊的移動範圍。若曲柄角度限制於某ㄧ範圍，連桿長度應該不會造成問題。但是如果曲柄要完成360度的旋轉，則連桿之間得長度須依其所能夠成之三角形關係而定。聯結桿長必須要比曲柄長。若有偏置情形時，則聯結趕與曲柄長度差應大於偏置距離e，當垂直狀態是最小距離。
當聯結趕和曲桿的差大於偏至距離e才會有兩個界限角，而界限角是當曲柄和聯結桿都在一直線上時，曲柄的水平角度。以滑塊為主動的時候，當曲柄轉到界限角的時候(連趕和曲桿重疊時候)滑塊就不能再往後運動，到達界限角之後，滑塊又往前運動。而曲柄到另一界限角角的時候(聯結桿和曲桿成ㄧ直線有最大距離)，不能再往前運動而就往後運動。

當聯結趕和曲桿差小於篇至距離e，而就只有ㄧ界限角聯結趕和曲桿成ㄧ直線有最長距離時)，而另一個界限角式不純在。因為當這種條件下曲桿不能選轉一圈，而最大旋轉範圍是當聯結桿與偏至距離e的方向上平行時(聯結桿垂直於水平面)。

而已知條件下R=10+(07)　L=R+5=23　e=10　L-R＜e 為第二種情況，因此上述分析而能做成動畫。

function [s,theta21,theta22]=slider_limit(R,L,e)
% P4.7   [s,th1,th2]=slider_limit(r)
%
% Find the stroke, extreme angles of link 2 in a slider mechanism system
% Input:R,L lengths of crank & connecting rod; e the offset of block
% Output: s:stroke, theta21:angle for the right position,
%         theta22:angle for the left position
% Examples:
%    [s,th1,th2]=slider_limit(5,12,3)
%
% Designed by D.S. Fon, BIME, NTU, Date:October 17,2002.
d2g=pi/180;
th1=asin(e./(R+L));
th2=asin(e./abs(R-L));
s=(R+L).*cos(th1)-abs(R-L).*cos(th2);
theta21=th1/d2g;
theta22=th2/d2g;

function [d,theta3]=slider_solve(theta2,R,L,e,mode)
% P4.8   [d,theta3]=slider_solve(theta2,R,L,e)
%
% Find the block coordinate and angle of connecting rod in a slider-crank system
% Input:R,L lengths of crank & connecting rod; e the offset of block
%       theta2: angles of crank, cane be a matrix
% Output: d:distance of the block from the origin.
%         theta3:angle of the connecting rod,
% Examples:
%    [d,theta3]=slider_solve(45,5,10,3)
%
% Designed by D.S. Fon, BIME, NTU, Date:Fegruary 9,2003.
if nargin<5, mode="0;end" d2g="pi/180;" theta="theta2*d2g;" cc="(e-R.*sin(theta))./L;">=0,
    theta3=asin(cc);
else
    theta3=asin(-cc)+pi;
end
d=L.*cos(theta3)+R.*cos(theta);
theta3=theta3./d2g;

上面程式為機動學光碟裡程式，運用上面程式再配合下面所寫程式即可畫出連桿

function slider_draw1(R,L,e)
%R為曲桿　L為聯結桿　e為偏至距離
%example:slider_draw1(17,23,10)
[s,theta21,theta22]=slider_limit(R,L,e)
thea2=asind((L-e)/R)+180;
ang=linspace(theta21,thea2,100);%分成１００個點
[d,theta3]=slider_solve(ang,R,L,e,1)
x=R*cosd(ang);
y=R*sind(ang);
for n=1:100
link_plot([0,x(n),d(n)],[0,y(n),e],2);%此為之前程式
line([d(n)-3,d(n)+3,d(n)+3,d(n)-3,d(n)-3],[e-2,e-2,e+2,e+2,e-2]);%畫出滑塊
axis equal
axis ([-45 45 -30 30]);
pause(0.01)
clf
end
thea3=asind((L-e)/R);
ang=linspace(thea2,-thea3,100);
[d,theta3]=slider_solve(ang,R,L,e,-1)
x=R*cosd(ang);
y=R*sind(ang);
for n=1:100
link_plot([0,x(n),d(n)],[0,y(n),e],2);
line([d(n)-3,d(n)+3,d(n)+3,d(n)-3,d(n)-3],[e-2,e-2,e+2,e+2,e-2]);
axis equal
axis ([-45 45 -30 30]);
pause(0.01);
clf
end
thea3=asind((L-e)/R);
ang=linspace(-thea3,theta21,100);
[d,theta3]=slider_solve(ang,R,L,e,1)
x=R*cosd(ang);
y=R*sind(ang);
for n=1:100
link_plot([0,x(n),d(n)],[0,y(n),e],2);
line([d(n)-3,d(n)+3,d(n)+3,d(n)-3,d(n)-3],[e-2,e-2,e+2,e+2,e-2]);
axis equal
axis ([-45 45 -30 30]);
pause(0.01);
clf
end
 
 
上述程式所做動畫如下(滑塊為主動)
 

若以老師講義的函式分析，當在使用sld_angle_limits時其中缺少了r3≧r4≧0,r3+r4≧r2，因此只要把
elseif r3+r4＞=r2 & r3＞=r4 & r4＞=0,
Qstart=-asin((r3-r4)/r2);
Qstop=pi+asin((r3-r4)/r2);
就能跑出正確答案。


曲桿為主動

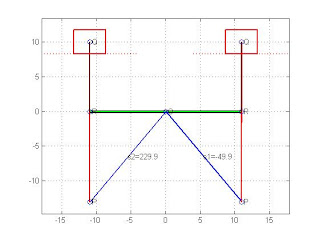
>> drawsldlimits([10,17,23,10],0,1,0)

Qstart =
-49.8808

Qstop =
229.8808

滑塊為主動

>> drawsldlimits([10,17,23,10],0,1,2)
Qstart =
-38.7298

Qstop =
38.7298

使用講義上的函式drawsldpaths(r6,th6,r,th1,td2,tdd2,sigma,npts,driver,mode)即可畫出連續圖形

第二連桿為主動(閉合型)

>> drawsldpaths(0,0,[10,17,23,10],0,10,0,1,100,0,0)
Qstart =
-49.8808
Qstop =
229.8808

第二連桿為主動(分支型)

>> drawsldpaths(0,0,[10,17,23,10],0,10,0,-1,100,0,0)
Qstart =
-49.8808
Qstop =
229.8808

閉合型和分支型的連續圖形極限位置角度相同，但是從上面兩圖中可看出圖形上有對偁。

滑塊為驅動桿(閉合型)

>> drawsldpaths(0,0,[10,17,23,10],0,10,0,1,100,2,0)
Qstart =
-38.7298
Qstop =
38.7298

滑塊為驅動桿(分支型)

>> drawsldpaths(0,0,[10,17,23,10],0,10,0,-1,100,2,0)
Qstart =
-38.7298
Qstop =
38.7298

講義上函式無法以滑塊為主做成動畫，因此只能畫出以曲桿為主動的動畫

曲桿為主動(閉合型)

曲桿為主動(分支型)

機動學HW8

Part1

P和Q兩點移動的範圍是一圓弧，因此速度方向是圓弧的的切線方向，所以P和Q點的速度方向是與連趕垂直，上圖就是如此標明。此圖的繪製是由function [values]=drawlinks(r,th1,th2,mode,linkdrive)程式中再呼叫function f4bar會製而成。

r=[4 3 3 5] (各桿之長度)

theta1 =0° (第一桿之水平角)

theta2 =45° (驅動桿之水平夾角)

td2 =10 (rad/sec) (驅動桿之角速度)

tdd2 =0 驅動桿(第二桿或第三桿)之角加速度(rad/sec^2)。

mode = -1 (閉合型)

linkdrive = 0 (驅動桿為第二桿)

[val,form]=f4bar([4 3 3 5],0,45,10,0,-1,0)

val =1.0e+003 *

Columns 1 through 5

0.0040 　　 0 0 　 0 0.0212 + 0.0212i

0.0021 + 0.0021i 0.0450 0.0100 0 0.0041 - 0.0245i

0.0011 + 0.0028i 0.0695 -0.0163 0.4914 -0.2121 - 0.2121i

-0.0008 + 0.0049i 0.0995 -0.0050 0.3836 -1.8712 - 0.4391i

Column 6

0.0021 + 0.0021i 0.0032 + 0.0049i00

form =1

四連桿之角度為

abs(val(:,2))'ans =0 45.0000 69.4856 99.5246

各桿之角速度則為

abs(val(:,3))'ans =0 10.0000 16.2681 4.9677

各桿之角加速度為

abs(val(:,4))'ans =0 0 491.4428 383.6120

速度和加速度為

abs(val(:,5))'ans =1.0e+003 *0.0300 0.0248 0.3000 1.9220

P和Q點到原點的距離

abs(val(:,6))'ans =3.0000 5.8635 0 0

Q節點之速度為30/s　
Q節點之加速度為300/s^2
Q點位置x=2.1　y=2.1
P節點之速度為24.8387/s
P節點之加速度為1922/s^2
P點位置x=3.2　y=4.9

P和Q點的以上的數據是用function [data,form] = f4bar(r,theta1,theta2,td2,tdd2,mode,linkdrive)算出數據，而上面數據是以MODE=-1的時候所得出的數據。如果要用程式直接標出速度和加速度方向，可用f4bar程式算出加速度和速度以向量型式表示在配合之前的founction four_link3 在P和Q點上畫出加速度(法限加速度和切線加速度)和速度方向向量。

Part2

上圖為連桿所能移動的最大範圍為，此時稱為極限點或是死點，是用function [h]=drawlimits(r,th1,sigma,driver)所畫出的圖形，在呼叫funtion f4bar，畫出連桿在極限點的位置。

>> drawlimits([4 3 3 5],0,-1,0)
Qstart =28.9550
Qstop =331.0450
ans = 154.0031 164.0026 165.0026 166.0026

Part3

上圖繪製的程式為

for theta2=0:20:360

drawlinks([4 3 3 5],0,theta2,-1,0)

end;

先由之前作業的grashof判定其連桿類型grashof(2,[4 3 3 5])ans =Non-Grashof Linkage此為雙搖桿型連桿，所謂的雙搖桿型是只第二桿和第四桿只能做有限度的轉動也就是所謂的擺動，當就無法做出旋轉一圈，故必然就有極限點的限制，就是搖桿所能轉動的最大的範圍且此死點位在第二桿為29度及331度時，一般成為死點或是極限點。當theta2=0:20:360 主動桿旋轉一圈時有些四連桿並無圖形，是因為當第二桿為29度及331度時之外的角度，是無法畫出四連桿的圖形，在程式4far之中在pos=B*B-C*C+A*A;小於零時是虛數無所謂的實數解，因此無法畫出連桿。

Part4

上面得動畫是由function move_4paths(r,r6,th6,nlink,th1,td2,tdd2,sigma,driver,ntimes,npts)繪製，由於此程式的呼叫函數，和內容過於龐大，所以只能短短說明，而帶入的參數為move_4paths([4 3 3 5],0,0,3,0,10,0,1,0,4,2)即可跑出動畫程式。


心得
(1)這次所程式大多是是講義內容上的而且程式過於繁多，而只是簡單的說明如何操作。
(2)有些程式雖然是講義上的，但是在matlab程式執行中會有小錯誤，因此要稍微的debug，修改程式的內容，如動畫製作要把move_paths程式稍作修改才可以執行。

機動學HW7

part1



當t=[ 1 2 3 4 5]端桿對應的方位，t=1到5要有五張圖片，因此直接做成動畫，直接呈現第一秒到第五秒的位置圖及移動。

dyad_amax 為畫出動畫的function

function dyad_amax(rho,theta,td,tdd,time)

%本函式呼叫dyad_draw
%在運用time為一矩陣，帶入角速度，角加速度公式
%ex: dyad_amax([7 12 2],[0 0 0 ],[0.2 0.5 0.3],[0 0.1 0.2],[1 2 3 4 5])
th=theta;
td1=td;
for i=1:length(time)%1到5秒的迴圈，輸入角速度和角加速度
for j=1:length(rho)
td1(j)=td(j)+tdd(j)*(i);%角速度公式
th(j)=theta(j)+td(j)*(i)+0.5*tdd(j)^2; %角度位移公式
end
[vel acc]=dyad_draw(rho,th,td1,tdd);%呼叫dyad_draw
for m=1:length(rho)
v(m,i)=vel(m); %把vel結果輸入到v的二維矩陣
a(m,i)=acc(m);%把acc結果輸入到a的二維矩陣
end
axis equal;
axis([-1 25 -1 20]);
pause(0.5);
end

part2

for j=1:length(rho)畫出時間與角速度與角加速度的關係
figure
hold on;
title('桿速度和加速度')
plot(v(j,:),'b--') %plot讀取二維矩陣畫出時間和速度的關析圖
plot(a(j,:),'ro-')
end


繪出三桿之結點之速度，加速度與時間t之關係

第一桿

第二桿

第三桿

機動學HW6

我有上本週（十二日）的課。
PART1



總共有12個連桿，其中滑塊也視為一連桿，滑動結和滑塊結都視為復式結所以連結度為二(f=2)，但是滑槽應該也是復式結，由於結點有4號和11號連桿，不是一個單純的滑槽結，算是一個稜柱結，因此連節度為一(f=1)。而其它結點都是旋轉結，自由度也都為一(f=1)，從圖中表面上只看到九個結點，但因多個連桿連結一個結點，所以不只九個結點，M、N、P、Q都為多個連桿的結點，因此帶入公式　　　　　　　　　　　　　　　　 　　

(結點數)=(連桿數-1)

M處為(3-1)=2；即連桿 3、6、8
N處為(3-1)=2；即連桿 7、8、12
P處為(3-1)=2；即連桿 2、3、4
Q處為(3-1)=2；即連桿 8、9、10
U處為(3-1)=2；即連桿 1、2、13
R處為(3-1)=2；即聯桿 4、9、13 滑結視為稜柱結連節度f=1
S、T處的滑動結和滑塊結都為復式結連節度f=2故種結點數為：

J=3(正常結)+2(M處)+2(N處)+2(P處)+2(Q處)+2(U處)+2(滑槽)=15

古魯伯公式是計算一個機構的可動度M，可動度要大於一或等於一，機構才可以運動，但是如果小於一的，則此機構是一個不可運動之結構，因此結構之間可能產生內力，互相做用。而計算方法：一個機構的可動度為總自由度減去拘束度，此方法為古魯伯(Grueber)公式

M = 3*(N-1)-(3J-Σf) = 3*(N-J-1)+Σf
N = 連桿之總數
J = 運動結之總數
i = 每一種連桿的連結度
因此我們就可以由古魯伯公式算出：
N=13 J=15 f=13*1+2*2=17
M=3*(13-15-1)+(17)=5

因此可動度為五。
jointype矩陣每個元素所代表：1 R型結 2 滑動結 3 複式結 4 球結 5 圓筒結 6 平面結 7 滾筒結 8 凸輪 9 螺旋結　10 球滑結 11 點觸結 所以有11個R型結，滑槽為特殊型式，因此是為滑動結，滑塊為復式結，連桿數為12所以(12,[11 2 2])算出M=5因此可動度為五。

function [df]=gruebler(nlink,jointype)%nlink為機構連桿數jointype為一矩陣
code=[1 1 2 3 2 3 1 2 1 3 5];%各種結的連結度(f)
n=length(jointype);%jointype的第幾個元素
dim=3;if n>3, dim=6;end; %因為n>3之後的為三度空間結點所以dim=6
ff=0;njoint=0; %設定出始值
for i=1:n,
    njoint=njoint+jointype(i);%加總所有連結點
    ff=ff+jointype(i)*code(i);%加總自由度
end;
df=dim*(nlink-njoint-1)+ff;%古魯伯公式

把數值帶入function
df=gruebler(12,[11 2 2])
上圖中，此機構的滑塊和滑槽都會增加此機構的可動度，滑塊可以做移動和轉動，如果滑塊固定，其結點與連桿能做轉動。滑槽也是如此滑槽的結點可以做移動和轉動，如果滑槽固定，其結點上的連桿能做轉動和移動。所以這兩種結點都會增加可動度。

PART2

從上圖中只有兩種形式的結點，一種為球型對(Spherical pair)或S-型對，球型隊必須維持兩接觸的球面之球心為共點，因此兩連桿連接時，將會被拘束在X、Y、Z軸方向上旋轉，無法作平移，雖然三度空間有六個自由度，但因為受限制減去三個平移的自由度，所以自由度為3，故DOF=3，拘束度也為三。另一種為圓柱對(Cylinddrical pair)或C型對，是維持兩鋼體之軸同線，兩鋼體間僅有一個軸向平移及一個垂直於軸之旋轉動運動，因此減去四個自由度，所以自由度為二DOF=2，拘速度為四。旋轉對只能在一個軸的方向上作旋轉，因此只有一個自由度，其它方向上都受限制，拘束度為五。

由於為三度空間古魯伯(Grueber)公式，所以要把本來二度空間的公式3個自由度改為6個自由度，其規則如下：
M = 6*(N-1)-(3J-Σf) = 6*(N-J-1)+Σf
因此旋轉結自由度為1，筒結自由度為2，球結之自由度為3。
上圖中，此機構有六個連桿，包含兩個旋轉結，一個圓筒結，三個球結。
N=6 J=6 f=2*1(旋轉結)+2*1(圓筒結)+3*3(球結)=13
M=6(6-6-1)+2*1+1*2+3*3=7
由matlab輸入df=gruebler(6,[2 0 0 3 1])
經過function運算之後df=7，可動度為M=7。
由於惰性自由度，實際可動度為M=7-3(軸向自轉)=4

結果經過Matlab算出的可動度與之前算出的的可動度一樣，但實際上可動度並不為七，因為被惰性自由度抵銷了，連桿３、５、６號桿都會發生軸向自轉。惰性自由度主要是由結點與結點之間連桿發生自轉所引起的，如六號連桿，因為是圓筒結所以可以自轉應該增加一自由度，但是另一結點接的卻是球結，造成連桿產生軸向自轉，因此不能算是一個自由度，但若在可自轉的該桿上在安插一桿，則將會增加自由度。

PART3

葛拉索機構在四連桿中，當最短桿與最長桿之和小於其他兩桿之和，則至少有一桿可為旋轉桿。此稱為葛拉索第一型。非葛拉所機構是指四連桿機構中，最長和最短兩桿的長度和大於其它兩桿長度之和，則所有三個活動搖趕必為搖桿或三搖桿機構，或稱為葛拉索第二型。

第一組：桿1-桿4分別為7,4,6,5cm
最長+最短=7+4=11
中桿長和=6+5=11
此為葛拉所變點機構或稱第三型，為葛拉索特殊狀況，最長桿合最短桿之和等於其他兩桿之和，連桿有兩種形式可繞一圈旋轉。

第二組：桿1-桿4分別為8,3.6,5.1,4.1cm
最長+最短=8+3.6=11.6
中桿長和=5.1+4.1=9.2
此為非葛拉所機構或稱葛拉索第二型，為三搖桿運動。

第三組：桿1-桿4分別為5.4,3.1,6.6,4.7cm
最長+最短=6.6+3.1=9.7
中桿長和=5.4+4.7=10.1
此為葛拉所機構
若鄰近最短桿之桿為基桿為曲柄搖桿型，因此6.6cm、5.5cm為基桿時，為此型。
若最短桿為基桿時，則基桿兩端之連桿為曲柄型，3.1cm為基桿，為此型。
若與最短桿相對應之連桿為基桿時，為雙搖桿型，4.7cm為基桿，為此型。


第一組
ans=grashof(1:4,[4 5 6 7])
ans = Neutral Linkage

第二組
ans=grashof(1:4,[3.6 4.1 5.1 8])
ans = Non-Grashof Linkage

第三組
ans=grashof(1,[3.1 4.7 5.4 6.6])
ans = Double-Crank Linkage

ans=grashof(2,[3.1 4.7 5.4 6.6])
ans = Crank-Rocker Linkage

ans=grashof(3,[3.1 4.7 5.4 6.6])
ans = Double-Rocker Linkage

ans=grashof(4,[3.1 4.7 5.4 6.6])
ans = Crank-Rocker Linkage

第一組
最長桿和最短桿之和要小於11，因此最長桿可減短或伸長，還是維持最長，最短桿也是可以伸長或減短，但還是要維持最短。

第二組
最長桿和最短桿之和要小於9.2，因此最長桿可減短或伸長，還是維持最長，最短桿也是可以伸長或減短，但還是要維持最短。

機動學hw5

part1

function body(L,theta,dd) %L=[L1 L2 L3]  theta=[theta1 theta2 theta3]為一矩陣,dd為手臂寬度
L1xt=L(1)*cosd(-theta(1)); %以[0 0]為原點算出上臂的終點
L1yt=L(1)*sind(-theta(1));
L2xt=L1xt+L(2)*cosd(-theta(1)-180 + theta(2));%以上臂的終點算出下臂的終點
L2yt=L1yt+L(2)*sind(-theta(1)-180 + theta(2));
L3xt=L2xt+L(3)*cosd(-theta(1)-360 + theta(2)+theta(3));%以下臂的終點算出手掌的終點
L3yt=L2yt+L(3)*sind(-theta(1)-360 + theta(2)+theta(3));
X=[0 L1xt L2xt L3xt];%把所有的x點放入X矩陣
Y=[0 L1yt L2yt L3yt];%把所有的y點放入Y矩陣
clf;
for i=1:length(X)-1  %從i=1到第4個X的element減一
A=[X(i) Y(i)]; %把X和Y第i個element帶入
B=[X(i+1),Y(i+1)];
g=0.5+i/2; %上臂長為g=1 ,下臂g=0.5+2/2 手掌g=0.5+3/2
if nargin==2,dd=1;end; %如果只放入兩個elemet,則dd=1
d=abs(dd);%算出距離
AB=(B(1)+j*B(2))-(A(1)+j*A(2));%轉換成複數座標
D=abs(AB);th=angle(AB);%算出距離，算出複數座標角度
t=linspace(pi/2,2.5*pi,20);%從pi/2到2.5*pi給予20個點
Cout=max(d/(2*g),0.2)*exp(j*t');Cin=Cout/2;%以複數形式畫圓cout畫大圓cin畫小圓
if dd>0,
    P=[0;Cin;Cout(1:10);D+Cout(11:20);D+Cin;D+Cout(20);Cout(1)];%畫出手臂的外為輪廓
else
    P=[Cin;0;D;D+Cin];%畫出手臂內的小圓(關節)
end
xx=real(P);yy=imag(P);%分別取實數部，何虛數部
x=xx*cos(th)-yy*sin(th)+A(1);%角度轉換
y=xx*sin(th)+yy*cos(th)+A(2);
line(x,y)
axis equal
axis([-50 50 -10 50 ])%固定座標軸
end;

圖案製作

L1=35; %上臂長
L2=30; %下臂長
L3=10; %手掌長
theta1=-90; %角度
theta2=-45;
theta3=-30;
try1([L1 L2 L3],[theta1, theta2 ,theta3],10); %帶入function

動畫製作

主程式呼叫body function

for d=0:1:10 %d=0到10
theta1=-90+1.5*d;
theta2=-45+d;
theta3=-30+2*d;
body([35 30 10],[theta1 theta2 theta3],4);%呼叫body function
pause(0.5);%每0.5秒暫停依次
axis equal;
end;

part2
2-1
除了拇指以外，其它四指從手掌與指頭連接的地方算起有三個關節，因此有三個地方可以旋轉，但由於人體關節的受限，關節當指節與指節身直時，假設角度為一百八十度，彎曲時最小角度可以達 九十度，所以只能在九十度到一百八十度之間移動。但事手掌與指頭連接的第一個關節比較特殊， 你會發現第一節關節的手指頭可以做三百六十度的旋轉，當然關節上還是有所限制不可能無限度做大幅旋轉。由於要討論手指間關節的自由度，因此我們把手掌視為不可以動的連桿，但連接指頭的第一關節到第三關節都可以移動，根據古魯伯公式M=3(N-J-1)+total(f)=>M=3(4-3-1)+3=3，有四個連趕(包括手掌)，有三個運動結，但我假設第一關節到第三關節都為旋轉(f=1)，如果第一關節當球對的話(f=3)，但假設都只能在平面運動的話都假設為旋對所以M=3有三個自由度，可以由三個指節做連桿運動。

2-2

把body function稍微改變一下，因為body function上臂、下臂、手掌有三個關節根手指一樣，因此只要稍微把主程式改過，就可以表現出手指最大的移動範圍 。

finger function 的主程式

f1j=linspace(-90,0, 20 ); %-90 到0設20個點
f1j2=linspace(180,90,20);
f1j3=linspace(180,90,20);
x=[1 -1 -1 1 1];
y=[0 0 -9 -9 0];
for t=1:1:4
if t==1 %當t==1執行食指的運動
  for d=1:1:20
  finger([2.5 2 3],[f1j(d) f1j2(d) f1j3(d)]);
  patch(x,y,'r');
  pause(0.1);
  end;

elseif t==2%當t==2執行中指的運動
  for d=1:1:20
  finger([2.5 2.5 3],[f1j(d) f1j2(d) f1j3(d)]);
  patch(x,y,'r');
  pause(0.1);
  end;

elseif t==3%當t==3執行無名指的運動
  for d=1:1:20
  finger([2 2 2.5],[f1j(d) f1j2(d) f1j3(d)]);
  patch(x,y,'r');
  pause(0.1);
  end;

elseif t==4%當t==4執行小指的運動
  for d=1:1:20
  finger([2 1.5 2.5],[f1j(d) f1j2(d) f1j3(d)]);
  patch(x,y,'r');
  pause(0.1);
  end;
end;
end;

2-3

根據手指的速度與加速度，假設手指速度固定而且手指的加速度是等加速度，因此可以較容易求出指頭的終端速度，由於每個人的手指長度不同，因此手指速度會不一樣，所以無法得知每個人投球時的指頭之間的速度，所以假設平均正常人能投時速一百公里的球，而且我們每個關節的相對速度和加速度會不一樣，因此我們考慮平均的速度和加速度，而且只考慮球真正被加速的時間，多餘的動作所花的時間應該排除，假設加速的時間為0.7秒，且投出時速100公里的球速。

           速度　　 角速度　　 角加速度

食指　　3.968kcm/s　529rad/s　755.7rad/s2
中指　  3.968kcm/s　496rad/s　708.6rad/s2
無名指　3.968kcm/s　610rad/s　871.4rad/s2
小指　　3.968kcm/s　661rad/s　994.2rad/s2

機動學hw4

part 1

part1 動畫

x=[0 17 17*cosd(60) 0];

y=[0 0 17*sind(60) 0];

line(x,y);

for d=0:30:360

x1 = x*cosd(d)+y*sind(d);

y1 =-x*sind(d)+y*cosd(d);

x2=17+x1;x3=x1+17*cosd(60);

y3=y1+17*sind(60);

line(x1,y1,'erasemode','xor','color','k');

line(x2,y1,'erasemode','xor','color','r');

ine(x3,y3,'erasemode','xor','color','y');

axis equal;

pause(0.5);

end;





part2

part2動畫

x=[0 10 10 0 0];

y=[2 2 -2 -2 2];

[a b]=scircle1(10,0,2,[-90 90]);

[a1 b1]=scircle1(0,0,2,[90 270]);

for i=0:30:360

x1=x*cosd(-i)+y*sind(-i);

y1=-x*sind(-i)+y*cosd(-i);

at=a*cosd(-i)+b*sind(-i);

bt=-a*sind(-i)+b*cosd(-i);

a1t=a1*cosd(-i)+b1*sind(-i);

b1t=-a1*sind(-i)+b1*cosd(-i);

Xs=[10*cosd(i) 15];

Ys=[10*sind(i) 0];

[p1 p2]=scircle1(10*cosd(i) ,10*sind(i),1 );

[p3 p4]=scircle1(0,0,1);line(x1,y1,'color','red');

line(at,bt,'color','red');line(a1t,b1t,'color','red');

line(p1,p2,'color','red' )

line(p3,p4,'color','red');

line(Xs,Ys);pause(0.5);

axis equal;

end;

part3
part3動畫


引用講義的旋轉function

import function:



function linkshape(A,B,dd)
if nargin==2,dd=1;

end;d=abs(dd);

AB=(B(1)+j*B(2))-(A(1)+j*A(2));

D=abs(AB);th=angle(AB);

t=linspace(pi/2,2.5*pi,20);

Cout=max(d/2,0.2)*exp(j*t');

Cin=Cout/2;if dd>0, P=[0;Cin;Cout(1:10);

D+Cout(11:20);D+Cin;D+Cout(20);Cout(1)];

else

P=[Cin;0;D;D+Cin];endxx=real(P);

yy=imag(P);x=xx*cos(th)-yy*sin(th)+A(1);

y=xx*sin(th)+yy*cos(th)+A(2);

line(x,y)

axis equal
----------------------------------------------------

for i=0:30:360

linkshape([10 0 ],[0 0],2);

linkshape ([0 0],[5*cosd(i) 5*sind(i)],3 );

linkshape([5*cosd(i) 5*sind(i)],[5*cosd(i)+10 5*sind(i) ],1.5);

linkshape([10 0],[5*cosd(i)+10 5*sind(i)],2);

pause(0.5);

end;

機動學HW3

part1

y=0:5:60;
plot (0,y,'-ro'),
hold on,
grid on; [a,b] = scircle1(0,0,30,[0 90]);
line (a,b);
b=0:2.5:30;
d=b.^2;
e=900-d;
a=e.^0.5;
plot (a,b, 'bo'), hold on ;
axis ([-10 40 0 70]);

如果依照題目手臂手肘只在二維上做平面運動，那拳頭就可以畫出一個大圓，是以手臂總長為半徑的大圓，如果是三維運動的話，理論上是可以畫出一個球體。但是人體肩膀和手肘都有關節上的運動轉動上的限制，因此要做此運動是不可能的，還有身體本身也是個阻礙，畢竟生物不是機械不可能做沒有自由度限制的運動。

part2

日常生活中高低對的運用是非常廣泛，而對低對點是指物體之間接觸面加大，因此單位面積受力較小，而相反的對高對而言，物理之間所接觸的面積是非長小的，可是是點之間或線之間的接觸，因此單位面積所受力較大，因此要挑選較能承受壓力的材質。平面低對包含了旋轉對和稜柱對，而旋轉對的用途很廣，如軸承、插梢、門閂旋轉對簡稱R型對(Revolute pairs簡寫)，而稜型對(P型對Prismatic pairs 簡寫)只能做一維的移動，如活塞，滑塊等等。下面網站介紹了許多種低對
http://www.cs.cmu.edu/~rapidproto//mechanisms/chpt4.html

有些低對可以由高對所取代，相同的高對也可以取代低對，高對的用在工業上非常廣泛，如滾珠軸承、滾柱軸承，雖然外型是旋轉對但內部是許多球對主合而成，像陪林也是高對一種運用，高對或低對都各有利弊，因此常常綜和各個優點組成複合式。不管高對或低對以上都是探討接觸的面積以及生活上的運用，但是要使連桿和結點之間保持所要的運動形式，要用某種方法使其固定，因此可以分為兩種形式，一種為外型式閉合，與外力閉合兩種。外型式閉和是以形狀加以限制連桿的運動方向，如活塞，軸承，轉軸，等等都是受方向上的限制，而外力式閉合，是受外力加以限制他運動方向，重力、壓力、彈力等等。但是一般都是以外型式閉和運較多，而且凸輪教適合此種運用。



part3



x=[78.554 0 0 11.11245 11.11245 -11.11245 -11.11245 0 0 -78.554 0 0 50.06035 0 -50.06035 0];


y=[61.8793 32.9556 39.62036 39.62306 61.87206 61.87026 39.62036 39.62036 32.9556 61.879 32.9556 0 -86.70707 0 -86.0707 0];


[a b]=scircle1 (0,0,10);


line(10*a,10*b,'color','red')


line(x,y);


for i=1:1:12


x1 = x*cosd(30*i) + y*sind(30*i)


y1 =-x*sind(30*i) + y*cosd(30*i)


x2= x1 + i*52.423077 c=10*a+i*52.423077;


d=10*b;


line(x2,y1);


line(c,d,'color','red');


axis equal;


end;



根據達文西人體的黃金比例，上半身/下半身的比=0.618，上半身跟下半身的分界是以肚臍，而雙手張開的手臂長，剛好就是一個人的身高，這就是黃金比例。

機動學hw2

part1

連桿機構是傳遞機械能的一種裝置，通常是由剛體構件用轉動副、移動副、球面副、球銷副、圓柱副或螺旋副中的一種或幾種聯結而成的機械機構，因為上述聯接副均屬於低副，連桿機構也稱為低副機構。通過不同的設計與計算，連桿機構可實現轉動、直線移動、往複運動和平面或空間的複雜函數運動軌跡。連桿機構設計包括軌跡實現、承載能力、結構設計等問題。最基本的連桿機構是平面四桿機構。

圖示

上圖是平面四連桿，所有運動副均為轉動副的四桿機構稱為鉸鏈四桿機構，它是平面四桿機構的基本形式。選定其中一個構件作為機架之後，直接與機架連結的構件稱為連架桿，不直接與機架連接的構件稱為連桿，能夠做整周迴轉的連架桿被稱作曲柄，只能在某一角度範圍內往複擺動的連架桿稱為搖桿。如果以轉動副連接的兩個構件可以做整周相對轉動，則稱之為整轉副，反之稱之為擺轉副。 鉸鏈四桿機構中，按照連架桿是否可以做整周轉動，可以將其分為三種基本形式，即曲柄搖桿機構，雙曲柄機構和雙搖桿機構。

活塞動畫

上圖為汽缸活篩之動畫，一開始動畫先介紹活篩與連桿是如何組裝，之後介紹汽缸是如何運動，當汽油點燃引爆，空氣膨脹推動活塞，而活篩做前後運動進而推動連桿，使連桿作搖擺運動，而整體而言是一個擺轉副運動，連桿連接軸承使軸承做迴轉運動因此可以運用在機械驅動方面上。

人體關節動畫
上方網址有頭顱、上肢、下隻3D動畫。3D動畫中上肢運動，如肩膀的關節是可以360度繞圈旋轉，但手軸只能180度的平面二維運動，但不可能選轉。肩膀可以作旋轉運動，再搭配上手肘可以做移動作用，經過互相配合可以進行複合運動，但是人體關節上必盡是有方向上限制，以及轉動跟移動上的限制，無法達到機械上旋轉或移動上的自由度。經由簡短介紹希望能多少暸接機械連桿的運動方式，以及運用上。

part2

工程設計之內成功的關鍵，無不在於設計中的創新，創新設計不只需要知識和經驗，更需要具有強烈的創意，和創新的思維，想像力比知識更為重要，因為知識是有限的，創新是一切進步的根源，但是要有天馬行空的創意畢盡是很少，因此一般人大部分，先把眾人的意見、問題、所要達成的目的等等，先集結起來，在經過眾人的討論，大家提出解決的方案，最後在經過討論分析來判定是否可行性。
具有設計的一般基礎知識外，更具備豐富的創造力，進而運用創造發明的能力，產生創新的構想與設計，根據Sternberg and Lubart (1995)所提出的創造力智慧三元論：「創造力需要合成能力（synthetic ability）、分析能力（analytic ability）及實作能力（practical ability）等三種能力平衡發展」，，需要合成能力、分析能力及實作能力等三種能力平衡發展，才能有效培養創造發明能力。因此要經過合成、 分析、實作等這些能力再加上已經所學的知是才能創新。從大一到現在學了這麼多科目，做了許多實驗，我們可以把記有的知識，經過分析整合之後，在經由實作來嘗試其可行性，經過不斷的努力，才會有創新的可能，創新之後經過實踐，把所要達成目標的機件與以發明出可以運用在實體當中。

下面網站是台大機械教授對創新發明的看法，以及提高學生創新的方法

網站

part3

>> M=7+10
M =
17
>> x=1:1:10
x =
1 2 3 4 5 6 7 8 9 10
>> y=x.^(1/M)
y =
Columns 1 through 8
1.0000 1.0416 1.0668 1.0850 1.0993 1.1112 1.1213 1.1301
Columns 9 through 10
1.1380 1.1450
>> plot(x,y)