機動學hw10

Part1

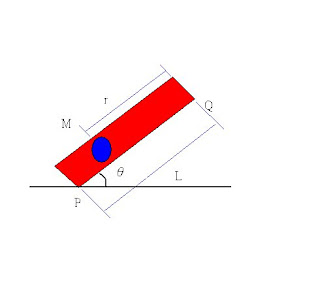
若以M為固定點，做逆時針旋轉，假設為等假角速度ω，則Vp=(ω) x (r)，若以複數座標表示iωr*exp(iωt+iθ)，而向心加速度為-(ω^2) x (r)以複數座標表示為-ω*ω*r*exp(iωt+iθ)。若從Q點看P點的速度為Vp=Vq +(ω) x (r)。若在M點有一水平速度，則P點速度為Vp=Vo + (ω) x (r) 若以複數座標表示v+iωr*exp(iωt+iθ)。若在M點同時有水平加速度，則P點速度為Vp=Vo+at+v+(ω) x (r)若以複數座標表示為v+at+iωＸ*exp(iωt+iθ)，加速度為a=a-(ω^2) x (r)，以複數座標形式為a-ω*ω*Ｘexp(iωt+iθ)。如果速度和加速度不為水平的，則只要分成水平方向和垂直方向。

四連桿的狀況
P以A為旋轉中心
Q以B為旋轉中心所以　
PQ　的速度方向　
如圖示都分別為桿子垂直方向

Part2

由於偏至量e為０，而若曲桿要旋轉一圈，則R>L，因此下面動畫是以R=15 L=20，而當曲桿與水平面垂直時，以機動課本圖，舜心１３點會交於無限遠。如動畫所呈現紅色圓圈為瞬心的位置

下面為畫出動畫的程式

%Example:slider_draw2(15,20,0)
function slider_draw2(R,L,e)
ang=linspace(0,360,100);
[d,theta3]=slider_solve(ang,R,L,e,1)
x=R*cosd(ang);
y=R*sind(ang);
for n=1:100
link_plot([0,x(n),d(n)],[0,y(n),e],2);
line([d(n)-3,d(n)+3,d(n)+3,d(n)-3,d(n)-3],[e-2,e-2,e+2,e+2,e-2]);
hold on
plot(0,0,'ro')
plot(x(n),y(n),'ro')
plot(d(n),e,'ro')
plot([0,0],[0,e-d(n)*(y(n)-e)/(x(n)-d(n))],'ro:') %算出瞬心點到連桿之間連線
plot([x(n),0],[y(n),e-d(n)*(y(n)-e)/(x(n)-d(n))],'ro:') %算出瞬心點連桿之間連線
plot([x(n),d(n)],[y(n),y(n)*d(n)/x(n)],'ro:')
plot([d(n),d(n)],[0,y(n)*d(n)/x(n)],'ro:')
axis equal
axis ([-45 45 -30 30]);
pause(0.05)
clf
end

以slider_draw2(15,20,0)跑出動畫為